Ebben a posztban algoritmuselmélettel, dinamikus programozással, és egy híres problémával fogunk foglalkozni.

• Az LCS probléma
  • Részsorozat?
  • Közös részsorozat?
  • Leghosszabb közös részsorozat?
• Az LCS probléma (még egyszer)
• A dinamikus programozásról általában
  • Általános technikák dinamikus programozásban
• Tervezzünk algoritmust!
• Alakítsuk át az algoritmust!

Valószínűleg mindenki, aki valaha is foglalkozott programozással, találkozott már olyan eszközökkel, ami két programkód közötti különbségeket képes kiemelni. Ezt a különbséget angolul diff-ként szokás emlegetni, ami sokat segíthet, ha például egy szöveg két változata közti különbségeket akarjuk megjeleníteni.

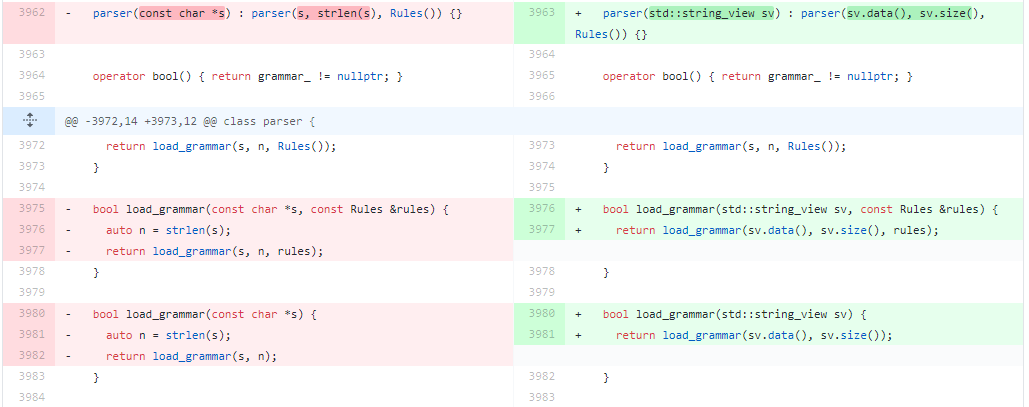
A képen egy nyílt forráskódú C++ könyvtár, a cpp-peglib két különböző állapota közti különbség látható. A bal oldali állapot az időben korábbi, a jobb olali pedig a későbbi állapotát mutatja a könyvtárnak. Ebben a konkrét esetben a C++ 2017-es szabványában megjelent string_view osztályt kezdték el használni a könyvtár fejlesztői. A konkrét változtatás, amiről a képet készítettem, itt érhető el.

Ahhoz, hogy a bal oldali állapotból a jobb oldali állapotba jussunk, a pirossal kiemelt sorokat előbb törölnünk kell, majd a jobb oldalon zölddel kiemelt sorokat hozzáadni a helyükre - ezt a diff-et a GitHub az LCS, avagy Longest Common Subsequence (Leghosszabb Közös Részsorozat) algoritmus segítségével állította elő.

Ebben a cikkben ezt a matematikai problémát, az LCS problémát fogom bemutatni, a megoldására két algoritmust bemutatva: rekurzív függvényhívásokkal, illetve dinamikus programozással. Mindkettő algoritmust C++ és C# nyelveken mutatom majd be, a teljes kód egy külön GitHub repositoryban elérhető.

Meg kell jegyezni, hogy a dinamikus programozás tulajdonképpen önmaga is egy rekurzív megoldási módszer, csak rekurzív függvényhívások helyett a korábbi eredményeket eltároljuk.

Az LCS probléma

Mielőtt az LCS problémát leírnánk formálisan, tekintsünk át néhány hozzá kapcsolódó fogalmat, és nézzünk meg pár egyszerű példát! Először az LCS rövidítés egyes szavainak jelentésével fogunk foglalkozni, utána pedig pontosan is definiáljuk magát a problémát. Nézzük a Leghosszabb Közös Részsorozat kifejezést hátulról!

Részsorozat?

Először is, mit jelent a részsorozat ebben a kifejezésben?

Vegyünk egy listát, és jelöljük a listát L-lel (a lista bármilyen elemeket tartalmazhat, lehet szó karaktekről, teljes szavakról, mondatokról, számokról vagy bármi egyéb adatról).

Ekkor ennek az L listának K részsorozata, hogyha az alábbi két feltétel teljesül:

• K minden eleme egyúttal eleme az eredeti L listának is
• K elemei az eredeti L listában ugyanolyan sorrendben követik egymást, mint ahogy K-ben

Fontos megjegyezni, hogy az K elemeinek nem kell feltétlenül közvetlenül egymás mellett állnia az eredeti L listában.

Vegyünk egy egyszerű példát: legyen L = ['A', 'B', 'C', 'D']. Soroljuk fel most L minden részsorozatát:

L 1 elemű részsorozatai:

• ['A']
• ['B']
• ['C']

L 2 elemű részsorozatai:

• ['A', 'B']
• ['A', 'C'] (!)
• ['A', 'D'] (!)
• ['B', 'C']
• ['B', 'D'] (!)
• ['C', 'D']

L 3 elemű részsorozatai:

• ['A', 'B', 'C']
• ['A', 'B', 'D'] (!)
• ['A', 'C', 'D'] (!)
• ['B', 'C', 'D']

L 4 elemű részsorozatai:

• ['A', 'B', 'C', 'D']

(!)-el jelöltem azokat a részsorozatokat, ahol legalább egy helyen van egy “ugrás”, avagy a részsorozat két szomszédos eleme nem volt szomszédos az eredeti L listában.

Megjegyzés:
Felmerülhet kérdésként, hogy miért beszélünk leghosszabb közös részsorozatról, ha egyszer listákat kezelünk. Természetesen létezik a részlista fogalma is, azonban ez a fogalom mást jelent. A részlisták esetében megköveteljük, hogy az eredetileg szomszédos elemek továbbra is szomszédosak maradjanak.
Ennek megfelelően a (!)-el jelölt listák nem lennének az eredeti L lista részlistái, ők csak részsorozatokat alkotnak L-ben. Ebben a cikkben a részlistákkal többet nem fogunk foglalkozni, azok egészen más feladatok megoldására hasznlhatóak.

Közös részsorozat?

Ha már tudjuk azt, hogy mi az a részsorozat, nem nehéz megérteni a közös részsorozat fogalmát se:

Vegyünk kettő listát, L1-et és L2-őt. Ekkor egy harmadik K lista közös részsorozata L1-nek és L2-nek, ha mindkettejüknek részsorozata.

Legyen például L1 = ['A', 'B', 'C'] és L2 = ['B', 'C', 'D']. Ekkor az alábbi részsorozatok találhatók meg mindkettő listában:

• ['B']
• ['C']
• ['B', 'C']

Leghosszabb közös részsorozat?

A fenti fogalmak birtokában a leghosszabb közös részsorozatot definiálni már igazán könnyű.

Vegyünk kettő listát, L1-et és L2-őt. Ekkor a két lista leghosszabb közös részsorozata az összes közös részsorozatuk közül a leghosszabb.

Legyen például megint L1 = ['A', 'B', 'C'] és L2 = ['B', 'C', 'D']. Azt már fent láttuk, hogy ennek a két listának 3 közös részsorozata van, ezek közül a leghosszabb: L' = ['B', 'C'].

Az LCS probléma (még egyszer)

Most, hogy a szükséges fogalmakat már átnéztük, definiálhatjuk magát az LCS problémát. Az előző fogalmak ismeretében ez már egészen egyszerű:

• A probléma bemenete: kettő lista, L1 és L2
• A probléma kimenete: L1 és L2 leghosszabb közös részsorozata

Persze felmerülhet kérdésként, hogy ha ismerjük két lista leghosszabb közös részsorozatát, abból hogyan tudunk egy olyan “diff” nézetet generálni, mint amit a fenti képen lehet látni. Ez egy picit nehezebb lesz, de egy olyan algoritmust fogunk tervezni, ami ezt a problémát is megoldja.

A dinamikus programozásról általában

Mint már írtam, az LCS probléma egy lehetséges algoritmikus megoldását dinamikus programozással fogom bemutatni. Érdemes röviden megemlékezni arról, hogy mégis mi az a dinamikus programozás. A dinamikus programozást az első számítógépek idejében, az 1950-es években egy Richard Bellman nevű matematikus dolgozta ki.

A módszer lényege a következő: egy matematikai problémára szeretnénk algoritmikus megoldást találni. A célunk az, hogy az eredeti problémát felbontsuk több, önmagához hasonlító kisebb problémára, majd azokat tovább bontsuk rekurzívan, amíg egy triviálisan megoldható problémát kapunk.

Ha valaki emlékszik a korábbi programozás tanulmányaira, akkor felidézhet hasonló algoritmusokat: elsőként a Fibonacci számsor, és a gyorsrendezés (quicksort) juthat eszünkbe. Ebből a kettő algoritmusból azonban csak az egyik, a Fibonacci számsor kiszámítása igazi dinamikus programozás:

• A Fibonacci számsor kiszámításakor az n. elem kiszámításához az n-1. és n-2. elem értékére van szükségünk. Ez a két részprobléma nehézségben és jellegében is hasonlít az eredeti problémára.
• A quicksort alkalmazásakor a kezdetben megkapott listát minden lépésben megfelezzük, és a kapott részlistákat rendezzük a quicksort rekurzív meghívásával. Ez a megoldás bár a quciksortot hívja meg rekurzívan, azonban a kapott új részproblémák jóval egyszerűbbek az eredetinél. Ez az oka annak, hogy nem tekintjük dinamikus programozási algoritmusnak a quicksort-ot.

Megjegyzés:
A fenti érvelést kissé pontosabban megfogalmazva: a dinamikus programozás esetén megköveteljük, hogy a keletkező részproblémák “átfedőek” legyenek.
Ez a Fibonacci számsor esetében teljesül: az n-2. elem kiszámítására mind az n-1., mind az n. elem kiszámítására szükségünk van. Így a könnyebb problémák “átfedésben” vannak egymással.
A quciksort esetén előbb a tömb első rendezését végezzül el, majd elkezdjük a résztömböket rendezni. Ekkor a résztömbök rendezése egymástól teljesen független feladat - az új részproblémák egymástól függetlenek. Emiatt ebben az esetben a részproblémák nem “átfedőek”.

Általános technikák dinamikus programozásban

Rengeteg különböző probléma van, amely megoldható dinamikus programozással, ám van néhány hasonló tulajdonságuk, amiket érdemes kiemelni:

• Megoldhatóak rekurzív függvényhívásokkal, vagy listákkal (tömbökkel).
  • A listák (vagy tömbök) általában a rekurzív függvényhívásokat helyettesítik.
  • Röviden: egy valós számítógépen a tárhelyigény növelésével egy algoritmus futásidejét csökkenthetjük (a köztes számítások eredményének tárolásával).
• A probléma bementét a legtöbb esetben minden rekurzív hívásnál 1 elemmel rövidítik le.
• A rekurzió végén a probléma egy olyan állapotba, amely már triviálisn megoldható.

Néhány közismert probléma, ami megoldható dinamikus programozással:

• Legrövidebb út keresés gráfban - Dijkstra algoritmusa is dinamikus programozást használ, csakúgy, mint a Bellman-Ford algoritmus.
• Az LCS probléma - nemsokára rátérünk a tényleges algoritmusra.
• Glob pattern matching - olyan egyszerű szöveges minták, amik '?' és '*' wildcard karaktereket tartalmazhatnak.
• Fibonacci számsor
• Hanoi tornyai

Tervezzünk algoritmust!

Eddig megfogalmaztuk az LCS problémát, átnéztük a dinamikus programozás általános ismérveit, és megismertünk néhány ismert dinamikus programozással megoldható problémát. Itt az ideje, hogy megtervezzük a tényleges algoritmust az LCS probléma megoldására!

Először koncentráljunk egy jelentősen egyszerűbb probléma megoldására: határozzu meg két lista leghosszabb közös részsorozatának hosszát! Ez jelentősen le fogja egyszerűsíteni a problémát, és ezt felhasználva magát a leghosszabb közös részsorozatot is meg tudjuk majd határozni.

Fent már említettem, hogy a dinamikus programozás során általában arra törekszünk, hogy a bemenetként kapott lista hosszát szépen lassan, egyesével csökkentsük, míg egy nagyon egyszerű esethez nem jutunk el. Hogyan tudjuk ezt megtenni ebben az esetben? A bemenet jelen esetben kettő listából áll, így nem lehet annyival elintézni a probléma egyszerűsítését, hogy “hagyjuk el a lista utolsó elemét”. Egy olyan problémát, aminek a bemenete kettő lista, összesen három féle módon lehetséges egyszerűsíteni:

• Az első lista végéről hagyunk el egy elemet
• A második lisa végéről hagyunk el egy elemet
• Az első, és a második lista végéről is elhagyunk egy-egy elemet.

A rekurzió során minden egyes lépésnél két listával dolgozunk, amik az eredeti listák rövidebb változatai. Egy rekurzív lépés során mindig az aktuális két lista utolsó kettő karakterét hasonlítjuk össze:

• ha az utolsó két karakter megegyezik, akkor úgy vesszük, hogy az benne van a leghosszabb közös részsorozatban - ekkor mindkettő lista végéről törölnünk kell egy-egy elemet, és a maradék listákra kell a rekurzív algoritmust meghívnunk
• ha ez a két karakter eltér, akkor meg kell néznünk, hogy mi történik, ha az első lista végéről törlünk egy elemet, és a második listát változatlanul hagyjuk; illetve fordítva. Eközül a kettő lehetőség közül pedig a hosszabbat kell választanunk.

Így tehát a célunk az, hogy ha az előbbb leírt három esetre már tudjuk a választ, akkor az eredeti kérdést is meg tudjuk válaszolni - az egyszerűsített problémákat pedig rekurzívan tovább egyszerűsítjük, amíg elérünk egy triviális esetet. A lehetséges egyszerűsítések mellett még meg kell határoznunk a triviális eseteket, amikor megállítjuk a rekurzív problémamegoldást. Általában, ha egy problémának egy lista (vagy esetleg több lista) a bemenete, akkor az üres, vagy egy elemű lista elérésére törekszünk. Így tehát a következő 2 triviális esetet mondhatjuk ki:

• Két üres lista leghosszabb közös részsorozatának hossza 0.
• Egy üres, és egy nem üres lista leghosszabb lista leghosszabb közös részsorozatának hossza szintén 0.

A következő ábrán egy rövid példán látható az algoritmus futása:

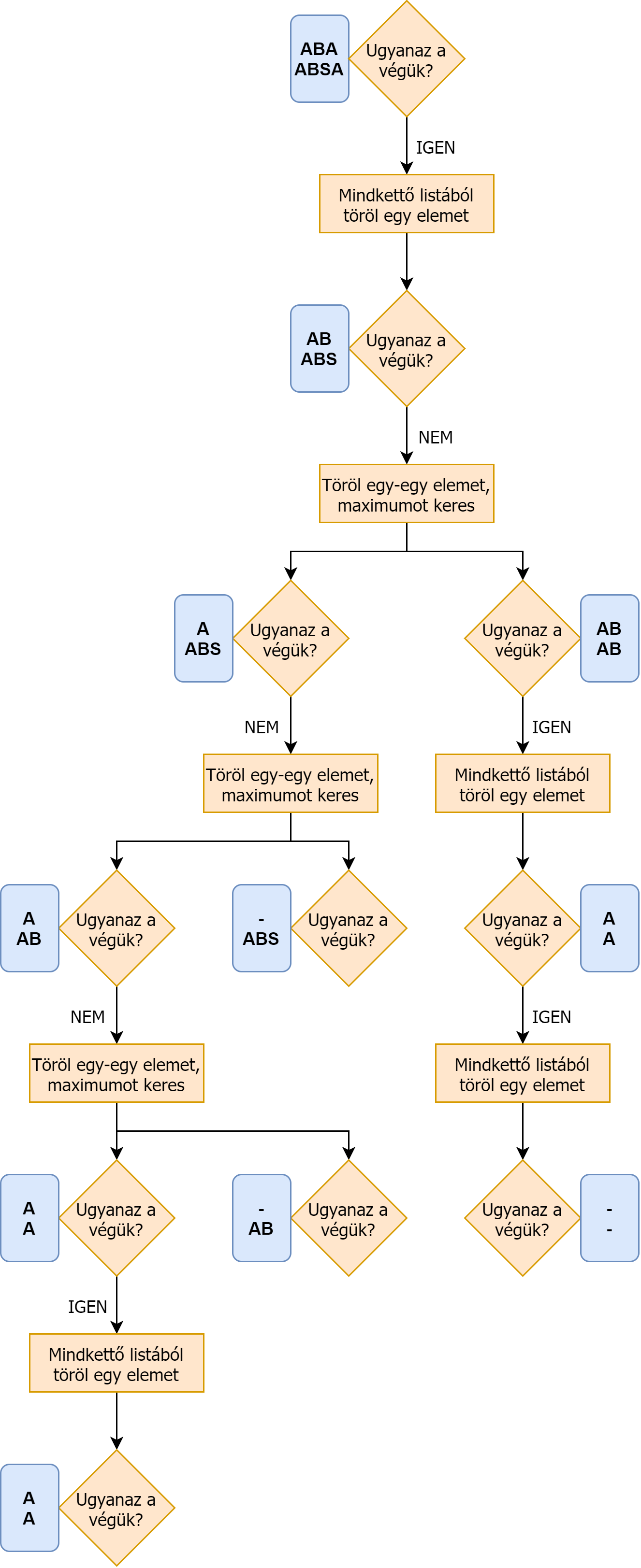
Ezzel igazából meg is vagyunk az algoritmus megtervezésével, már csak annyi maradt hátra, hogy lekódoljuk magát az algoritmust. Ezt először rekurzív függvényhívásokkal fogjuk elvégezni, majd a rekurzív függvényhívások helyett egy kétdimenziós tömbben tároljuk el a részeredményeket. A rekurzív algoritmus tehát a következőképpen fog kinézni, C++ nyelven megírva:

template<typename TYPE>
int lcs(std::list<TYPE> const & list1, std::list<TYPE> const & list2)
{
  if(list1.empty())
    return 0;
  if(list2.empty())
    return 0;

  auto list1_shorter = list1;
  auto list2_shorter = list2;
  list1_shorter.pop_back();
  list2_shorter.pop_back();

  if(list1.back() == list2.back())
  {
    return lcs(list1_shorter, list2_shorter);
  }
  else
  {
    int len1 = lcs(list1, list2_shorter);
    int len2 = lcs(list1_shorter, list2);
    return len1 > len2 ? len1 : len2;
  }
}

Ez a kód természetesen nem optimális, hiszen a rövidebb listák képzéséhez előbb lemásolja mindkettő listát, majd a pop_back tagfüggvény meghívásávl törli ki az utolsó elemet. Ehelyett sok más optimális megoldás elképzelhető, a C++ nyelvhez legjobban illeszkedő megoldás az lenne, ha egy-egy iterátorpárt kapna az lcs függvény, ami két konténer első elemét, illetve a végét jelezné. Ekkor figyelnünk kell arra, hogy a C++ nyelvben a .end() tagfüggvény mindig az utolsó utáni elemre mutat - ahhoz, hogy az utolsó elemet megkapjuk, egy elemmel hátrébb kell lépnünk. Az előző kód átírása után ezt kapjuk:

template<typename ITERATOR>
int lcs(ITERATOR begin1, ITERATOR end1, ITERATOR begin2, ITERATOR end2)
{
  if(begin1 == end1)
    return 0;
  if(begin2 == end2)
    return 0;

  if(*(end1 - 1) == *(end2 - 1))
  {
    return lcs(begin1, end1 - 1, begin2, end2 - 1);
  }
  else
  {
    int len1 = lcs(begin1, end1, begin2, end2 - 1);
    int len2 = lcs(begin1, end1 - 1, begin2, end2);
    return len1 > len2 ? len1 : len2;
  }
}

Ez a kód már jól működik, és már majdnem meg tudjuk határozni a leghosszabb közös részsorozatot:
Azok az elemek, amelyek az algoritmus által megtalált leghosszabb közös részsorozatot alkotják, mindig szerepelnek az if elágazás true ágában - ha ezeket az elemeket összegyűjtjük, megkapunk egy lehetséges leghosszabb részsorozatot. Ezzel a megoldással az a probléma, hogy a rekurzív hívás miatt egy-egy elemet többször is vizsgál a függvény, így a végeredményben is többször szerepelne.
A függvény másik problémája, hogy borzasztó lassú - pont mint abban a klasszikus esetben, amikor a Fibonacci számsor elemeit rekurzívan számoltuk ki. A megoldás itt is hasonló lesz: a részeredményeket egy táblázatban fogjuk eltárolni, és az alapján állapítjuk majd meg a végeredményt.

Alakítsuk át az algoritmust!

Ha egy matematikai problémára már megalkottunk egy rekurzív hívásokkal dolgozó algoritmust, azt (egy kis gyakorlattal) már gyerekjáték átalakítani úgy, hogy a részeredményeket egy tömbben tároljuk el! A tömbről először három dolgot kell megállapítanunk:

• hogy milyen típusú elemeket tárolunk majd el benne,
• hogy hány dimenziós legyen (azaz hány indexe legyen),
• és hogy mekkora legyen a tömb mérete az egyes dimenziók mentén.

Ha az eredeti algoritmust/függvényt ismerjük, akkor általában már könnyű dolgunk van:

• a tömbben lévő elemek típusát azonnal láthatjuk a függvény visszatérési értékéből. Mivel a fenti C++ függvény int-tel tér vissza, így mi is int-eket fogunk majd eltárolni.
• A tömb dimenziója egy picit bonyolultabb kérdés, és a fenti függvény paramétereinek számával áll szoros összefüggésben. Azonban az első esetben kettő, a második esetben 4 paramétere volt a függvénynek, így erre nem lehet ránézésre egyértelmű választ adni. Azonban ha visszagondolunk az LCS probléma eredeti megfogalmazására, azt mondtuk, hogy “A probléma bemenete: kettő lista”. Így a négy paraméteres függvény is igazából 2 “logikai” paramétert kap, csak azok a C++ sajátosságai miatt 4 technikai paraméterré változnak. Ez alapján tehát a tömb két dimenziós lesz.
• Az utolsó teendőnk a tömb méretének a meghatározása a két dimenziója mentén. Ha listákkal dolgozunk, akkor a tömb mérete a legtöbb esetben közvetlen összefüggésben áll a lista méretével - vagy azzal egyezik, vagy annál egyel nagyobb. A mi esetünkben az utóbbi lehetőség lesz hasznosabb - a 0-ás index a korábbi leállási feltételnek fog majd megfelelni. Így a tömb első indexe 0-tól az első lista elemszámáig terjed majd, a második index pedig 0-tól a második lista elemszámáig.

Azt tehát már tudjuk, hogy a tömb hogy fog kinézni, és hány eleme lesz. Azonban érdemes egy picit elgondolkodni, hogy a tömb egyes cellái ténylegesen milyen értéket fognak tartalmazni:

• Az alapötlet az egész tömbbel az, hogy megfordítjuk a rekurzió irányát. Az előző függvényekben rögtön a legbonyolultabb feladattal akartunk kezdeni, két lista leghosszabb részsorozatának a hosszát akartuk meghatározni. Most, a tömbös megoldásnál fordítva fogunk gondolkodni - meghatározzuk a táblázat minden elemét, a legegyszerűbbektől kezdve.
• Ha táblázatként képzeljük el magunk előtt ezt a tömböt, akkor a jobb alsó elem persze a végeredményt tartalmazza - azaz az eredeti listák leghosszabb közös részsorozatának hosszát. Amikor a rekurzív hívásban egy-egy elemet töröltünk a listák végéről, tulajdonképpen a listák hosszát csökkentettük.
• Így tehát a tömb egyes cellái az eredeti listák rövidebb “részlistáira” fogják meghatározni az LCS probléma megoldását.
• Kicsit pontosabban: a tömb első indexe az első listához tartozik, a második index a második listához. Ha az első index értéke i, a másodiké pedig j, akkor a tömb [i,j]-edik eleme az első lista első i, illetve a második lista első j eleméből alkotott listák leghosszabb közös részsorozatának hossza.
• Vegyünk egy konkrét példát:
  • A listák álljanak karakterekből.
  • L1 = "I <3 dynamic programming."
  • L2 = "Algorithm theory is not that hard."
  • Az eredményeket tároló tömb pedig legyen: int result[][]
  • Ekkor a result tömb 4. sorának 3. eleme az "I <3" és az "Alg" stringek leghosszabb közös részsorozatának hossza.

Már csak annyi van hátra, hogy kezeljük a triviális eseteket, illetve kitaláljuk, hogy hogyan töltsük ki a nem triviális eseteket. Mik lesznek itt a triviális esetek? Természetesen ugyanazok, mint korábban - a 0 elemből álló listák. Így a végeredményt tároló tömböt kezdetben 0-kkal töltjük fel minden olyan helyen, ahol valamelyik index 0.
A nem triviális esetekben pedig a korábbi rekurzív híváshoz hasonló módon kell eljárnunk, azonban rekurzív hívás helyett itt a tömb kisebb indexű elemeit fogjuk használni:

• Amikor az aktuális utolsó karakterek megegyeznek, mindkettő listából törölni kell egy-egy elemet. Ezt a tömbös megoldásnál úgy tudjuk elérni, hogy mindkettő indexet csökkentjük, és megnézzük hogy mi van az általuk jelölt cellában.
• Amikor az utolsó karakterek nem egyeztek meg, akkor két hívást kellett elvégezni - egyszer az első listából töröltünk egy elemet, a második alkalommal pedig a másodikból. Ekkor a tömbben az aktuális elemtől egyel “feljebb”, illetve az egyel “balra” álló elemet fogjuk majd megnézni. Ez annak felel meg, mintha külön-külön kivonnánk egyet az indexekből, és a kapott két elem közül keresünk maximumot.

Ezek alapján egy teljes, működőképes kód:

#include <iostream>
#include <string>
#include <algorithm>

template<typename ITERATOR>
int lcs(ITERATOR begin1, ITERATOR end1, ITERATOR begin2, ITERATOR end2)
{
  auto len1 = end1 - begin1; // count of elements in the first list
  auto len2 = end2 - begin2; // count of elements in the second list

  // creating the temporary array
  int** tmp = new int* [len1 + 1];
  for (auto i = 0; i <= len1; ++i)
    tmp[i] = new int[len2 + 1];
      
  // initializing the temporary array
  for (auto i = 0; i <= len1; ++i)
    tmp[i][0] = 0;
  for (auto j = 0; j <= len2; ++j)
    tmp[0][j] = 0;

  auto i = 1;
  for (auto it1 = begin1; it1 != end1; ++it1)
  {
    auto j = 1;
    for (auto it2 = begin2; it2 != end2; ++it2)
    {
      if (*it1 == *it2)
        // if the last elements are the same, go back in each direction
        tmp[i][j] = tmp[i - 1][j - 1] + 1;
      else
        // if the last elements are different, select max in the two directions
        tmp[i][j] = std::max(tmp[i - 1][j], tmp[i][j - 1]);
      ++j;
    }
    ++i;
  }

  auto result = tmp[len1][len2];

  for (auto i = 0; i <= len1; ++i)
    delete[] tmp[i];

  delete[] tmp;

  return result;
}

int main()
{
  std::string str1 = "I <3 dynamic programming.";
  std::string str2 = "Algorithm theory is not that hard.";

  auto length = lcs(str1.begin(), str1.end(), str2.begin(), str2.end());
  std::cout << "The longest common subsequence of '" << str1 << "' and '" << str2 << "' is " << length << " long" << std::endl ;
}

Ha a fenti programban szereplő ideiglenes tömböt kiírjuk a konzolra, a következő eredményt kapjuk:

     A l g o r i t h m _ t h e o r y _ i s _ n o t _ t h a t _ h a r d .
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
I  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
_  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
<  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
_  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
d  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3
y  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3
n  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3
a  0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4
m  0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4
i  0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4
c  0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4
_  0 0 0 0 0 0 1 1 1 1 2 2 2 2 2 2 2 3 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5
p  0 0 0 0 0 0 1 1 1 1 2 2 2 2 2 2 2 3 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5
r  0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 4 4 4 4 5 5 5 6 6 6
o  0 0 0 0 1 1 1 1 1 1 2 2 2 2 3 3 3 3 3 3 4 4 5 5 5 5 5 5 5 5 5 5 6 6 6
g  0 0 0 1 1 1 1 1 1 1 2 2 2 2 3 3 3 3 3 3 4 4 5 5 5 5 5 5 5 5 5 5 6 6 6
r  0 0 0 1 1 2 2 2 2 2 2 2 2 2 3 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 6 6 6
a  0 0 0 1 1 2 2 2 2 2 2 2 2 2 3 4 4 4 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 6 6
m  0 0 0 1 1 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 6 6
m  0 0 0 1 1 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 6 6
i  0 0 0 1 1 2 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6
n  0 0 0 1 1 2 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 6 6
g  0 0 0 1 1 2 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 6 6
.  0 0 0 1 1 2 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 6 7